Want access to my FREE resource library? Click here to join!
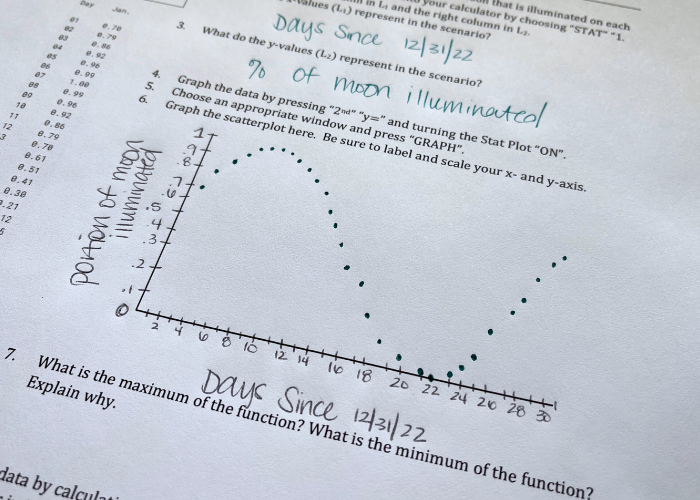
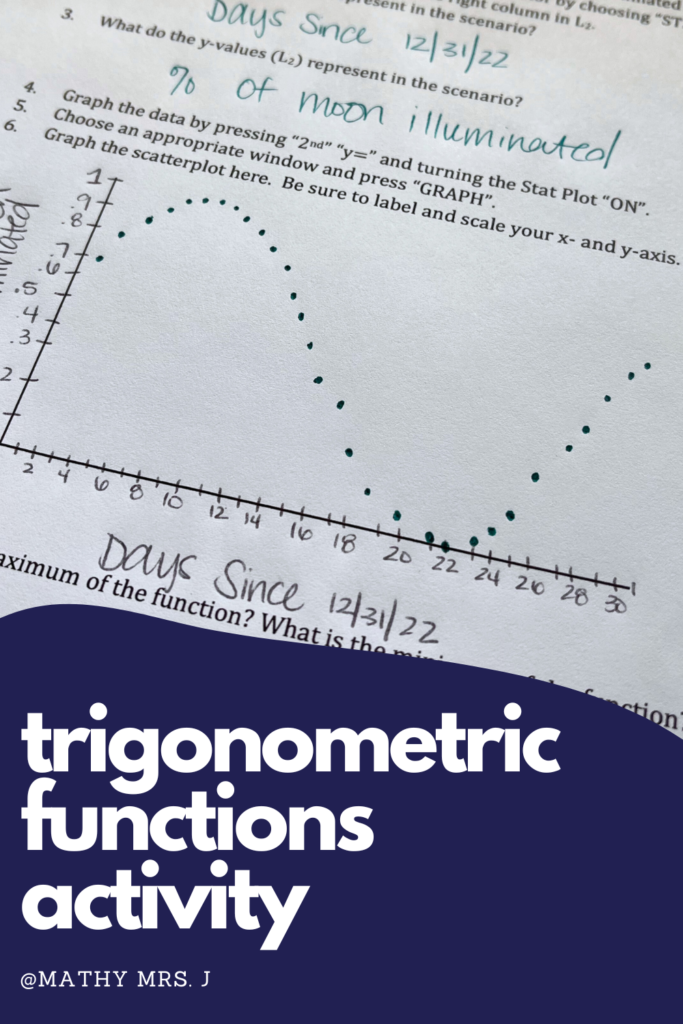
I taught trigonometric functions for the first time in my 5th year of teaching. I incorporated some of the classic activities, such as the spaghetti lesson, and it got me so excited about how trigonometric functions can be applied to real world situations. As it turns out, the phases of the moon follow a periodic model! More specifically, the portion or percentage of the moon that is illuminated every 24 hours can be modeled with a sine or cosine function.

Creating the Real World Trigonometric Functions Activity
So, what to do with that information? First, find data of the percentage of the moon that’s visible over a 30 day period. This website publishes the data, and it’s from the military so it seems pretty reliable to me! Just choose the dates you want to find data for and it will return the information. Use the day of the year as the x-value of the function, and the percentage of the moon illuminated as the y-value of the function.

If you provide data for the beginning of the year, then students can build an equation that models the relationship between the date and the percentage of visible moon for the whole year. There are options for how to build the equation.
- Use knowledge of the altitude, period, frequency, and midline of a sine or cosine function to write the equation by hand. (My resource on TpT walks students through this process and includes the answer key!)
- Use a calculator to find a regression equation for the data
- Or, do both of these and compare the results to see how similar they are.
Add Rigor to the Activity
Now that students have a trigonometric function that models the data of the percentage of the moon illuminated over time you can elevate their understanding through rigorous questions. Use the following questions to get students thinking more deeply about the content.
- What percentage of the moon will be illuminated on x date?
- When is the next full moon?
- How many new moons will there be this year?
- Is x date a good day for stargazing?
- Is there enough moonlight for a nighttime walk next Tuesday?
- Some coral species show an increase in spawning in greater amounts of moonlight. When do you expect the next increase in coral spawn?
This project increases students’ understanding of trigonometric functions by providing a real world situation that students can really dive into! It’s also great for honors classes to provide an extra challenge. If you use this activity let me know how it goes! Leave a comment or find me on social media: @mathymrs.j
Don’t forget to request access to my FREE resource library – click here!
Happy teaching!
Natasha